[techaday:0004] Fresnel積分と緩和曲線

2015-11-27

はじめに

突然ですが，**「高速道路のインターチェンジや線路のカーブを作ってください」**と言われたとするとあなたならどうしますか？ほとんどの人は，まず一番オーソドックスな円弧を考えると思います．しかし，少しだけ考えてみてください．直線と円弧のつなぎ目は連続で1階微分可能でこそあれ，微分した結果は不連続になり，2階微分は不可能ですね．これはつまり，カーブに差し掛かった時に急ハンドルを切らなければならないということに相当します．このままではあなたが設計した道路は事故多発地点になってしまいます．それでは一体どのようにカーブを作ればよいのでしょうか？というのが今日の話題です．

前提知識

微積分の計算ができる
高校物理の力学がわかる

効能

車両ロボットなどの軌道・経路計画をする際に慎重になる
数学がちょっと役立てられている場面を知ることができる

動機

冒頭に挙げた高速道路のインターチェンジの問題への解答はこうです：

曲率が連続となるような曲線(緩和曲線)を作ればよい

非常にシンプルで抽象的な解答ですね．とはいっても曲率とは一体なんぞやとか，どうしてそれでいいのかとか，具体的にどうすればいいのかといった疑問が生じてくると思います．それを見ていきましょうというのが今回の趣旨です．簡単のため平面曲線について扱い，より一般の空間曲線についてはまた機会があれば書くことにします(キーワードとしては捩率でしょうか)．

曲率

曲率には直観的(古典的)定義と微分幾何学的定義とがありますが，今回は直観的定義に基づいて話を進めていきます．まず，微小な曲線は円弧に近似できるものとします．

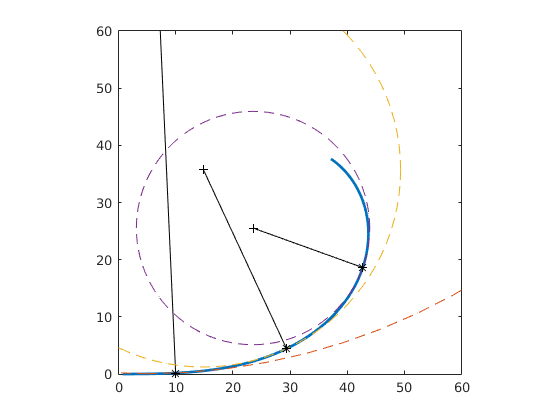
このとき，ある点周辺の微小曲線を近似した円弧の半径を曲率半径 $r$ ，その逆数を曲率 $\kappa=\frac{1}{r}$ と定義します．直線の場合の曲率半径は便宜的に $r = \infty$ とします．すなわち曲率 $\kappa = 0$ です．

曲率半径と曲率は，曲線の形状によって決まり(曲率が曲線の形状を決めるとも言えます)，曲線上のどの点を選ぶかによって変化します．

直線と円弧の組み合わせでは，曲率半径が $\infty$ から不連続に円弧の半径 $r_1$ に変化します．つまり，ハンドルを0度の状態から急に20度とか30度に不連続に変化させないと，この経路は通れません．

向心力・遠心力との関係

力学的にも考えてみましょう．向心力・遠心力については，高校物理等でご存知の方が多いと思います．質量 $m$ の物体が円運動しているとき，ある時刻での移動する速さを $v$ ，円運動の半径を $r$ とすると，円の中心方向に引っ張る力(向心力)が $$ F = m \frac{v^2}{r} $$ のようにはたらくというものです．

ここで注目してもらいたいのが $\frac{1}{r}$ の部分です．これって曲率ですよね！つまり，速度を一定とすると，向心力は曲率に比例します．車に乗っている人の気持ちになると，遠心力が曲率に比例することになります．曲率が不連続に変化するということは，車体横向きに急に力がかかったり外れたりすることに相当します．そんな乗り心地の悪い道，嫌ですよね．

Cornu螺旋・クロソイド曲線・Fresnel積分と緩和曲線

さて，話を戻しましょう．ここまでで，直線と円弧の組み合わせでは急ハンドルを切らなければならない，遠心力が急にかかって乗り心地が悪くなる，ということが幾何的側面と力学的側面からわかりました．

では一体どのようにカーブを設計すればよいのでしょうか？最もシンプルなアプローチはハンドルを一定速度で回しながら通れる経路を考えるというものです．仮にハンドルを無限に回せるものとして，一定速度で切り続けるとどのような軌跡を描くのか，プロットするとつぎのような螺旋になります．

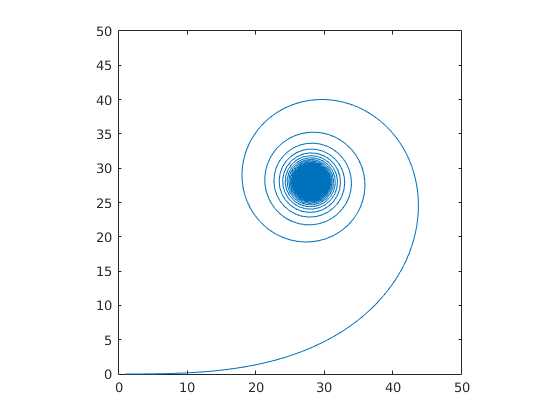
美しい模様ですね．これはCornu螺旋と呼ばれる曲線の一種です．特に，曲率が1次関数で記述できるものをクロソイド曲線と呼びます(こっちのほうが有名？)．

この曲線はつぎのような式で表されます． $$ C(s) = \int_0^s \left( \cos\left(\int \kappa(\sigma) d\sigma \right), \sin\left(\int \kappa(\sigma) d\sigma \right) \right) d\sigma $$ ここで，$\kappa(\sigma) = \sigma$ とすると， $$ C(s) = \int_0^s \left( \cos\left(\frac{\sigma^2}{2} \right), \sin\left(\frac{\sigma^2}{2}\right) \right) d\sigma $$ となります(積分定数は0とした)．さて，問題は $\cos(\sigma^2), \sin(\sigma^2)$ の積分です．こいつらはどうやっても初等関数で(積分を使わずに)表現できないことが知られています．これらの関数を Fresnel積分 (cos, sin に対応付けて FresnelのC,S とも) と呼びます． $$ \mathcal{C}(s) = \int_0^s\cos(\sigma^2) d\sigma $$ $$ \mathcal{S}(s) = \int_0^s\sin(\sigma^2) d\sigma $$

ちなみに，曲線の長さを計算すると， $$ L(s) = \int_0^s \sqrt{\left(\frac{dx}{d\sigma}\right)^2+\left(\frac{dy}{d\sigma}\right)^2} d\sigma = \int_0^s \sqrt{\cos^2\left(\frac{\sigma^2}{2}\right)+ \sin^2\left(\frac{\sigma^2}{2}\right)} d\sigma = s $$ となり，曲線の長さは $s$ と等しくなります(定義から明らかといっちゃ明らかです)．

Fresnel積分の値は簡単には計算できません．つまり，曲線の長さに相当するパラメータ $s$ を与えたところで，終端位置は計算が難しいのです．でも安心してください．数値的に近似値を求める方法がいくつかあります．

数値積分(誤差が怖い)
関数近似(これとかこれとか)

気になる方は調べてみてください．ロボット等で使用する場合は，現実的には予め計算して数値テーブルか何かで持っておく必要がありそうです．私は少し違った表現方法で曲線の形状を格納しているため，直接計算することはしていません．それについてはまた後日．

緩和曲線は，このような曲率が連続となる曲線の総称を指し，道路や線路に広く用いられています．

まとめ

曲率と車両の運動の関係についてイメージできるようになった
背景にある数学的豆知識を手に入れた

参考

補足

微分幾何学的には，$s$ が曲線の長さと等しくなるようなパラメータ $s$ を弧長パラメータと呼びます(厳密な定義は割愛)．
Fresnel積分の定義には定数がかかったりかからなかったりいろいろと流派があるようです．Fourier変換とかと似たものを感じますね．
緩和曲線だけではハンドルをぐるぐる回しっぱなしになってしまうので，大抵の道路では緩和曲線の区間から曲率が連続になるように円弧につないで(ハンドルの角度は固定)，カーブの終わりに差し掛かるとまた緩和曲線を使って直線につなぐということがされています．